This delightful, oh-so-lyrical topic was suggested on Facebook by my husband, Mark Dennehy. Why? I’ll ask him and get back to you at the end of this post. However, let us make a start, shall we?
The first starting point in researching this is Wikipedia. Your intrepid blogger goes and enters this in the search box and gets the following definition;
A pseudo-Riemannian “metric” is a nondegenerate quadratic form on a real vector space Rn.
Okay… that didn’t really help very much. What about a Riemannian metric? Wikipedia gives me the following;
ARiemannian metric is a positive-definite quadratic form on a real vector space.
Huh. I’m still in the dark here. So what is in fact a quadratic form?
A Quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,
is a quadratic form in the variables x and y.
Well, now at least we’re on more familiar ground. I recognise the style of equation given. Is it possible that we’re looking at a nomenclature for a form of mathematics that I’m already familiar with?
Lets have a look at the definition for a homogeneous polynomial. What does that tell us?
A homogeneous polynomial is a polynomial whose nonzero terms all have the same degree
Ok, that didn’t really help. However, do you notice the definitions are getting shorter? It is almost as if we’re getting closer to a form of definition we might just understand. This is very much a cause of hope, a cause of optimism. We’re on the case and we’re getting closer. Maybe too close…. Okay, stop being silly. Lets see what the definition of a polynomial brings us. Is that one smaller again?
A polynomial is an expression of finite length constructed from variables (also called indeterminates) and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents.
Ah for feck’s sake!
Yeah but hang on, though. This seems almost understandable and familiar. 2 + 2 would be a polynomial, according to this definition. Right, so now we’re getting somewhere. Let’s go back, and have a look at the definition above this.
A homogeneous polynomial is a polynomial whose nonzero terms all have the same degree
The same degree… without being cubed or squared? So our example of 2 + 2 would seem to still be valid. So what was the one above that?
A Quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,
is a quadratic form in the variables x and y.
So a Quadratic form seems to relate to the equation where the variables are squared. Okay, I’m balancing my understanding on a shaky tray, but it’s still hanging in there. So what’s the next one?
ARiemannian metric is a positive-definite quadratic form on a real vector space.
Crashing into a brick wall. I’m guessing that this is stating the equation they are speaking of is not a minus (i.e., -2y would not be included) and by the same logic would not be grafted on the -x\y section of the graft. Very much guess work here, though. However, there’s only one more definition to go. This is the Boss Level, the big cheese, the whole enchilada.
A pseudo-Riemannian “metric” is a nondegenerate quadratic form on a real vector space Rn.
Nope, I’m back to giving you blank stares. But with a burst of inspiration, I put ‘Pesudo-Riemannian’ into Google Images, and this is what you get;

From http://coldcreation.blogspot.ie/
Which suggests that these equations are of use in describing huge, unknown tracts of space, that they help us to understand the unknown, that they can do a universe more than my stupid efforts can perceive. They see what we can’t.
Sometimes I hate being so obtuse.
Still no clear response from hubby regarding why he suggested this topic. If he gives me a reason I’ll update this entry.
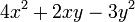
knowing your hubby as well as I do, I can pinpoint the approximate point in this blog where he will (in his oh-so-quiet manner) start to, how shall I put this nicely, “wibble” at your math (because, apparently it’s “math” not “maths”… no, I don’t understand his logic on that one either!)….. ya see that word “equation” right up there…. that’ll give him all sorts of grief…. I can hear him in my head ranting aimlessly about the lack of an “=” sign, so therefore it can’t be an equation, blah, blah, blah, yadda, yadda, yadda 😉
oh, btw, I’m trying to come up with something to counteract his proposed calculus for infants malarky!
The reason for the lack of an = sign is that he has made me switch to a new laptop with a German keyboard that has cleverly hidden the = sign on me. I blame Merkel meself, it’s clearly a trap.
I do suspect his reasons for suggesting this topic may, just may, have something to do with the reasons you suggest. But I love my Maths equations, yes I do! *shakes ringlets, hugs stuffed toy, giggles, topples over*
“balancing my understanding on a shaky tray”: brilliant
I’m not sure but I think its R^n and not Rn.
Also it’s also more fun to say the pseudo-Riemannian properties can be determined by the product of the Hessian because then you think of old headless Prussian-esque knights having a math-off in a battlefield.